Ejercicios Cuarto Parcial
Ejercicio 1
Ajuste polinomios de primer y segundo grado a los puntos:
| N° | $X_n$ | $f(x_n)$ |
|---|---|---|
| 1 | 1 | $f(x_0) = 0$ |
| 2 | 4 | $f(x_1) = 1.386294$ |
| 3 | 5 | $f(x_2) = 1.609438$ |
| 4 | 6 | $f(x_3) = 1.791759$ |
Evalúe ambos en x = 2 Para el polinomio de segundo grado:
Interpolación de Newton
| i | $x_i$ | $f(x_i)$ | Primer | Segundo | Tercer |
|---|---|---|---|---|---|
| 0 | 1 | 0 | $\frac{1.386244 - 0}{4-1} = 0.462098$ | ||
| 1 | 4 | 1.386244 | $\frac{1.609438 - 1.386244}{5-4} = 0.223144$ | $\frac{0.223144 - 0.462098}{5 - 4} = -0.238954 $ | |
| 2 | 5 | 1.609438 | $\frac{1.791759 - 1.1609438}{6-5} = 0.182321$ | $\frac{0.182332 - 0.223144}{6-5} = -0.040812$ | $\frac{1.791759-1.609438}{6-5}=0.182321$ |
| 3 | 6 | 1.791759 |
Ejercicio 2
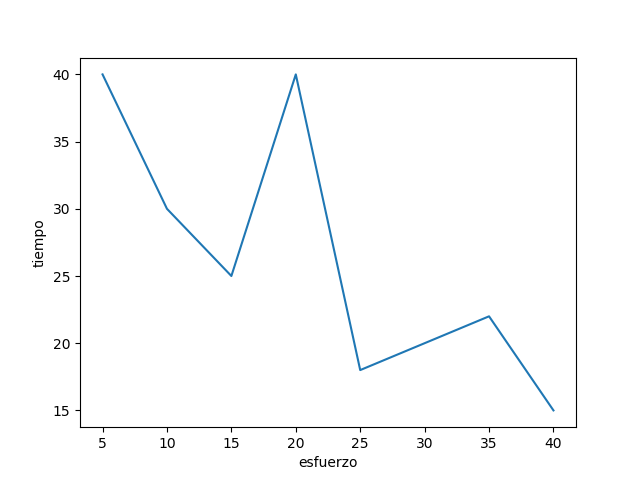
Se realiza un experimento para definir la relación entre el esfuerzo aplicado y el tiempo para que se fracture cierto tipo de acero inoxidable. Se aplican 8 valores distintos de esfuerzo, y los datos resultantes son:
| Esfuerzo aplicado, $kg/mm^2$ | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
|---|---|---|---|---|---|---|---|---|
| Tiempo para la fractura $t$ | 40 | 30 | 25 | 40 | 18 | 20 | 22 | 15 |
Estime el tiempo de fractura para un esfuerzo aplicado de:
- $13 kg/mm^2$ es de: 25.44
- $28kg/mm^2$ es de: 17.8560
Ejercicio 3
El volumen específico de un vapor sobrecalentamiento se enlista en tablas de vapor para distintas temperaturas. Por ejemplo, a una presión absoluta de 3000 $lb/in^2$ se tiene
| T, °f | 700 | 720 | 740 | 760 | 780 |
|---|---|---|---|---|---|
| V, ft/lb | 0.0977 | 0.12184 | 0.1406 | 0.15509 | 0.016643 |
Polinomio de segundo grado Con polinomio de 3er grado para T=750 (desde 720 hasta 780) = 0.14830875
Ejercicio 4
El número de habitantes (en miles) de una determinada ciudad ha evolucionado según la siguiente tabla:
| Años | 1987 | 1988 | 1989 | |
|---|---|---|---|---|
| Población | 53 | 71 | 91 |
Sabiendo que dicha población se ajusta a una función cuadrática, calcularla población que tenía la ciudad en 1985.
Interpolación de Newton
| i | x | f(x) | Primero | Segundo |
|---|---|---|---|---|
| 0 | 1987 | 53 | ||
| $f[x_1, x_0] = \frac{71 - 53}{1988 - 1987} = 18$ | ||||
| 1 | 1988 | 71 | $f[x_2, x_1, x_0] = \frac{20-18}{1989 - 1987} = 1$ | |
| $f[x_2, x_1] = \frac{91 - 71}{1989 - 1988} = 20$ | ||||
| 2 | 1989 | 91 |
Interpolación de Lagrange
Primer grado: 17 Segundo grado : 23
Ejercicio 5
Resuelve la ecuación diferencial: desde $x = 0$ hasta $x=4$ con $h=0.5$
La condición inicial en $x=0$ es $y=1$
| i | $X_i$ | $Y_i$ | $f(X_i, Y_i)$ |
|---|---|---|---|
| 0 | 0 | 1 | $f(x_i.y_i) = f(0, 1)= 8.5$ |
| 1 | 0.5 | $Y_1 = 1 +8.5 * 0.5 = 5.25$ | $f(x_i, y_i) = f(0.5, 5.25) = 1.25$ |
| 2 | 1 | $Y_2 = 5.25 + 1.25 * 0.5 = 5.875$ | $f(x_i, y_i) = f(1, 5.875) = -1.5$ |
| 3 | 1.5 | $Y_3 = 5.875 - 1.5 * 0.5 = 5.125$ | $f(x_i, y_i) = f(1.5, 5.129) = $-1.25 |
| 4 | 2 | $Y_4 = 5.125 -1.25 * 0.5 = 4.5$ | $f(x_i, Y_i) = f(2, 4.5)$ = 0.5 |
Ejercicios 6
Resuelve el PVI
$Y’ = 4e^{0.8x} - 0.5y$ en $[0, 4]$, con un tamaño de paso $h=0.5$, con condiciones iniciales de $x=0$, $y=2$
| i | $x_i$ | $y_i$ | $f(x_i,y_i)$ | $y_i+1(0)$ | $f(x_i+1,y_i+1(0))$ | SOLUCION VERDADERA |
|---|---|---|---|---|---|---|
| 0 | 0 | 2.000000 | 3.000000 | 3.500000 | 4.217299 | 2.000000 |
| 1 | 0.5 | 3.804325 | 4.065136 | 5.836893 | 5.983717 | 3.751521 |
| 2 | 1 | 6.316538 | 5.743895 | 9.188485 | 8.686225 | 6.194631 |
| 3 | 1.5 | 9.924068 | 8.318434 | 14.083285 | 12.770487 | 9.707042 |
| 4 | 2 | 15.196298 | 12.213981 | 21.303289 | 18.904580 | 14.843922 |
| 5 | 2.5 | 22.975938 | 18.068255 | 32.010066 | 28.087673 | 22.427014 |
| 6 | 3 | 34.514920 | 26.835245 | 47.932543 | 41.812316 | 33.677172 |
| 7 | 3.5 | 51.676811 | 39.940182 | 71.646901 | 62.306670 | 50.411772 |
| 8 | 4 | 77.238524 | 59.510859 | 106.993953 | -49.496977 | 75.338963 |
Ejercicios 7
Resuelve el problema de valor inicial $\frac{dy}{dx} = 4e^{0.8x} - 0.5y$ en $[0,4]$ con valores iniciales para $x = 0$ y $y = 2$, con un tamaño de paso $h = 1$
| i | $x_i$ | $y_i$ | $k_1$ | $k_2$ | $k_3$ | $k_4$ |
|---|---|---|---|---|---|---|
| 0 | 0 | 2 | 3.000000 | 4.217299 | 3.912974 | 5.945677 |
| 1 | 1 | 6.201037 | 5.801645 | 10.830056 | 9.572954 | 14.025653 |
| 2 | 2 | 16.306590 | 11.658835 | 25.641516 | 22.145845 | 32.019783 |
| 3 | 3 | 39.515480 | 24.334965 | 58.694846 | 50.104876 | 72.077683 |
| 4 | 4 | 91.850829 | 52.204706 | 132.341761 | 112.307497 | 161.238851 |
| 5 | 5 | 208.974508 | 113.905346 | 296.327138 | 250.721690 | 359.680825 |
| 6 | 6 | 470.255146 | 250.914097 | 661.360443 | 558.748857 | 801.331201 |
$Y_{0+1}= 2 + \frac{1}{6} (3 +2(4.127299) + 2(3.912974) + 5.945677)(1) = 6.201037$
Operaciones
| Operaciones para primer “intervalo” | Resultado de K |
|---|---|
| $K_1 = f(0,2) = 4e^{0.8(0)} - 0.5(2) = $ | 3 |
| $K_2 = f(0 + \frac{1}{2}(1), 2+\frac{1}{2}(3)(1) ) = f(0.5, 3.5) = 4e^{0.8(0.5)}-0.5(3.5) = $ | 4.217299 |
| $K_3 = f(0 + \frac{1}{2}(1), 2+\frac{1}{2}(4.217299)(1)) = f(0.5, 4.103650) = 4e^{0.8(0.5)}-0.5(4.183650) = $ | 3.912974 |
| $K_4 = f(0 + 1, 2 + 3.912974(1)) = f(1, 5.912974) = 4e^{0.8(1)}-0.5(5.912974) = $ | 5.945677 |
Ejercicio 8
Si la resistencia del aire es proporcional al cuadrado de la velocidad instantánea, entonces la velocidad $v$ de una masa $m$ que se deja caer desde cierta altura se determina por: Sea $v(0) = 0$, $k = 0.125$, $m = 5 slugs$ y $g = 32$ pies/$s^2$. Use el método de RK4 con $h = 1$ para aproximar la velocidad $v$(5).
| $i$ | $X_i$ | $Y_i$ | $K_1$ | $K_2$ | $K_3$ | $K_4$ |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 32.000000 | 25.600000 | 27.904000 | 12.534170 |
| 1 | 1 | 25.25702827 | 16.052063 | 4.305948 | 13.217294 | -5.006837 |
| 2 | 2 | 32.93898006 | 4.875590 | 0.712095 | 4.286029 | -2.642532 |
| 3 | 3 | 34.97719755 | 1.414891 | 0.165156 | 1.270303 | -0.847033 |
| 4 | 4 | 35.55032704 | 0.404356 | 0.043959 | 0.365275 | -0.248261 |
| 5 | 5 | 35.71275425 | 0.114980 | 0.012241 | 0.104050 | -0.071086 |
| 6 | 6 | 35.7588334 | 0.032646 | 0.003455 | 0.029557 | -0.020223 |
| 7 | 7 | 35.77190794 | 0.009265 | 0.000979 | 0.008390 | -0.005743 |
| 8 | 8 | 35.77561787 | 0.002629 | 0.000278 | 0.002381 | -0.001630 |
Solución analítica